This tweet was favorited, retweeted, and/or responded to at least 20 times after I posted it last night. Teachers everywhere feel this. I couldn’t decide if all of the attention made me feel slightly better, or worse.
So, the math review topic could not have come at a better time for me. For some crazy reason, I decided to grade tests on a Friday night. It was a “round up” type of test covering important topics from pre-algebra this year; evaluating algebraic expression (involving order of operations), exponents, exponent rules, combining like terms, and multi-step equation solving. The good news is my students have finally learned to use parenthesis when substituting values for variables and can solve equations LIKE MAD. The bad news? They are apparently mystified by the order of operations, especially within the vicinity of any sort of exponent rule problem. I felt so defeated after grading those tests. I failed. After my dog used me as a trampoline in the middle of the night, I could not go back to sleep thinking about it. I do so much to help them learn math, but what am I helping them do to remember it? I have failed.
The most common math mistake that I encountered was:
Students had order of operations issues and just wanted to distribute things. Michael, here come.
What happened? First, I HATE PEMDAS. This starts early, and students are already brainwashed by 6th grade when I get them. I teach my students GEMS instead of PEMDAS but all of the GEMS in the world can’t seem to fix this. I hate PEMDAS because students see parenthesis and go into “I must do that first” mode, even when there is only ONE number inside the parenthesis. Just because it is in parenthesis, one number, for example (2), does NOT a group make. I must frequently emphasize this, because very few students made this error when there was just one number in the parenthesis. But, this knowledge did not transfer when they had two numbers. The distributive property trumped all. They do love to distribute. They also distributed the exponent to both numbers inside the parenthesis. I have no idea why they would do this, because I don’t even teach them the power to a power exponent rule. I have them expand any set of parenthesis with an exponent. They do love the distributive property, but we-e have never, ever, ever, distributed an exponent. Sigh. I failed.
This year things are worse than before because our classes are shorter than last year. I have replaced my daily warm-up review with “Make a new page in your notebook and update your TOC”. It’s been awesome for our INB, but obviously tragic for the Order of Operations. So, starting Monday, I am going to have one problem of the day for both classes posted on the board. It will look like a variation of this. Evaluate -3x^2 – 2x + 5 when x = -2. I’ll throw in fractions, decimals, and any other basic, easily forgettable concept. This should help them quickly practice evaluating algebraic expressions, exponents, and the order of operations, EVERYDAY. And we will go over it, together, everyday.
I will NOT go down, without a fight.
What are YOU doing to review past math topics? What are YOU doing to help them remember what they have learned?


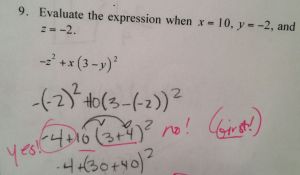
Have you tried discussing the “Dead Puppy Theorem”? I don’t know if 6th grade is too young to get it, and you may scar them for life, but the shock may help them remember. I did that this year (with seniors in HS cause they make the same mistakes!), only to realize that we were moving away from algebra for a while, so the DPT became history.
Another thing I’ve done, stolen from elsewhere on the web, is the “Board of Remediation”–basically a giant board at the back of the room with practice worksheets on every “easily forgettable concept” as you put it. If I were more with-it as a teacher, I’d go grab one of those every time I saw a student make a mistake (instead, I use it in my Participation Points scheme–students can do those if they feel they need the practice, and some students take me up on it!).
I don’t think I’ve heard of the “Dead Puppy Theorem”. Tell me more please! And, I love your participation points! But, I’m underwater as it is this year and don’t have the courage to go there this year! I can just dream about it!
Ooh, so the BoR doesn’t require PPs–it’s actually really easy to setup and here’s where I found it from:
Meanwhile, here’s the DPT (although you could really create any super-common-frustrating error to become the DPT):
http://bowmandickson.com/2012/11/06/the-dead-puppy-theorem-and-its-corollaries/
Would it help the students not just to practice *evaluating* expressions, but also to focus explicitly on the structure of expressions? In my view, PEMDAS is about *interpreting* expressions, and without appropriate interpretation, there won’t be correct evaluation!
Here’s one way to focus on the structure of expressions. This is taken from Mathematics for Elementary Teachers with Activities, 4th edition, by Sybilla Beckmann, published by Pearson (page CA-180):

/Users/sybilla/Desktop/Screen Shot 2013-03-23 at 9.52.35 PM.png
[I can’t tell if this figure will show up. Therefore I will make a related posting on the Mathematics Teaching Community, at
https://mathematicsteachingcommunity.math.uga.edu
where I will be able to post the figure]
By the way, a strength of the Common Core State Standards, I think, is standards that ask students interpret expressions and understand how expressions are composed of their component parts (e.g., Standard for Mathematical Practice 7 and 6.EE.2b and at high school, the domain “seeing structure in expressions”).
Finally, don’t be too hard on yourself! Even college students make the kinds of errors you described. It seems to be very difficult to break students from applying rules that seem intuitively correct but are not mathematically valid.
The posting at
https://mathematicsteachingcommunity.math.uga.edu/index.php/448/interpreting-algebraic-expressions
now has the picture I referred to above. It shows a way to focus on the *structure* of an expression (rather than just evaluating straight away).
I’d be interested in hearing comments about this method! (Please post any on the Mathematics Teaching Community!)
I like the visual breakdown of the structure, but it’s a little confusing (no doubt because I’m not getting the explanation). One thing I suggest to students is that when they see (x + 1)^2 that they think “Oh, F…….oil!” and that the “square” means x + 1 times x + 1 and that whole distributive property thing, and that half the class will get it wrong and make the teacher want to set their paper on fire (or whatever version of the Dead Puppy THeorem I’m using ;)) and they can pick to be in the half that makes the teacher sigh with relief and smile.
Pingback: How To Review Past Math Topics | I Speak Math
Why are we all up so early when we have no school today??? Like a SHOT, I sat up in bed at 4:30 am. Love your ideas! Hope to hear and share more since I have the same issues!!
Each week I create 2 Daily Math worksheets. They consist of 8 problems each, and review several topics we’ve learned throughout the year. Eight problems make it manageable to grade, but it really tells me what mistakes continue to occur and what my students remember. I rarely grade homework for correctness, but in this case, I tell my students that this is content previously learned , so there are no excuses for incorrect answers! They can use their math notebooks or any other resource to answer a question they forget how to do. Some have learned this the hard way, but I really think it has helped material retention!
Pingback: “I have no idea why they would do this” | Productive Struggle
I spend a fair amount of time repeating that PEMDAS is about doing what is *in* the parentheses – that they’re like a fence, or wrapping paper around a problem.
I try to use the same language when the same thing comes up… I’ll explain that math folks are so efficient/lazy that they decided that “if we don’t tell you what to do, multiply” — so things that are next to each other get multiplied, and a number before parentheses around something means we’ll be multiplying — **unless** there’s some other directions there. The “next to things so you multiply” thing comes up rather often…
I like how you use the word directions as well as you fence analogy and will be incorporating both. Thanks!
Funny, I also often talk about efficient (lazy) mathematicians. I usually start with lazy and then bring it around to efficient. They get a kick out of it.
If you don’t like PEMDAS, can you offer some suggestions for a middle school math teacher who is currently teaching evaluation of expressions, order of ops, and prop. of operations. I don’t want to set them up for failure in high school. Thanks! 🙂
I’m sorry. Hate was definitely too strong of a word. I’ll never grade tests in a Friday night after a looooooong week again! I like GEMS bc it takes the word parenthesis out. But I’m in the minority. Almost everyone uses PEMDAS. I posted about GEMS before, I should have linked to it. I’ll add it tonight. Thanks! 🙂
I used GEMS this year. Some of them really got into it. Since the rule was that they couldn’t draw a gem unless they had written out the initials and crossed them off one at a time as they worked, at least they kept them in order, which they struggle with when using PEMDAS.
10(3 + 4)^2 is tricky! PEMDAS or GEMS, strictly speaking, says “do 3+4, get 7, square that, and then multiply by 10,” which works and gets the right answer every time. But there are other ways to “see” 10(3 + 4)^2… what do we do with the kids who see other ways? How do we help them know which ways of seeing are right, which are wrong, and why?
Other right ways to see it:
10 * (3 + 4) * (3 + 4)
(30 + 40)(3 + 4)
10(3^2 + 14 + 4^2)
10 * 7 * 7
70 * 7
Wrong ways to see it:
10 * 3^2 + 4^2
10 * 3^2 + 10 * 4^2
(30 + 40)^2
30 + 4^2
34^2
70^2
I wonder if some version of “the mistake game” or “my favorite no” in which kids know what the answer should be, based on some authority like a calculator or just being told the answer, and then they have to figure out what steps were done to get each wrong and right expression, and why those steps were wrong?
Also, how do we know we’re interpreting expressions right? One way is to think of the clearest way to tell someone what you want them to do, and see if they’re equivalent. Like, if I wanted someone to get 70^2 from 10, 3, 4, and squaring, I’d need to do (10(3+4))^2. A way to play with this is to play games like the 24 game where you give some values and operations and use grouping symbols and order of operations to get as many values as possible and check them with each other.
A rule I like to use is “you can’t practice until you can find and fix your own mistakes” — and once you can find and fix your own mistakes, then you have to practice a lot so you go from making mistakes that you catch to feeling that dzzzzt! when you’re about to make a mistake.
Order of operations is tough because it’s not as logical, it’s more about convention, and so learning to a) get it automatic through practice with quick feedback and b) recover gracefully when you do see it wrong at first (which I still do!) are both important!
It sounds like your kiddos are learning to do both things, and just ’cause they don’t always do it on Friday’s quizzes doesn’t mean they aren’t learning tons!
Thanks so much Max for all of your great advice and suggestions! I did just one problem a day last week at the beginning of class. Each student read out their answer. It was GREAT that they all made mistakes bc they could see everyone was having trouble and didn’t feel like it was “just them” making a mistake. This really opened the doors for them and we went around the room each day identifying where they had made their mistake. It was a great discussion! We did this everyday and by day 4, almost every student was getting the right answer! I will definitely keep this up, for many different topics. I think that identifying each students mistakes and talking about it really helped. Plus, more practice never hurts. I do have that 24 game. That’s a great idea too! 🙂
I’ve been using My Favorite No for bell work. I only do one problem a day, which means reviewing during bell work is a strategic decision that means giving up the chance to quickly assess if kids can do the stuff they are currently learning. Doing more than one problem a day leads to behavior issues for my first class of the day, and I don’t really have the energy right now to mix up bell work each period.
Other teachers in my school are spending this crucial time before the state standardized test doing small groups of review questions for bell work. I would love to do this, but it will have to be another year for me.